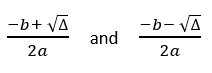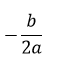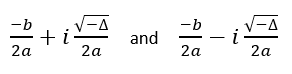Write a C program to find all roots of a quadratic equation using if else. How to find all roots of a quadratic equation using if else in C programming. Logic to find roots of quadratic equation in C programming.
Input
Input a: 8 Input b: -4 Input c: -2
Output
Root1: 0.80 Root2: -0.30
Required knowledge
Basic C programming, Relational operators, If else
Quadratic equation
Wikipedia states, in elementary algebra a quadratic equation is an equation in the form of
![]()
Solving quadratic equation
A quadratic equation can have either one or two distinct real or complex roots depending upon nature of discriminant of the equation. Where discriminant of the quadratic equation is given by
![]()
Depending upon the nature of the discriminant, formula for finding roots is be given as.
- Case 1: If discriminant is positive. Then there are two real distinct roots given by.

- Case 2: If discriminant is zero then, it has exactly one real root given by.

- Case 3: If discriminant is negative then, it has two distinct complex roots given by.

Logic to find all roots of a quadratic equation
Based on the above formula let us write step by step descriptive logic to find roots of a quadratic equation.
- Input coefficients of quadratic equation from user. Store it in some variable say a, b and c.
- Find discriminant of the given equation, using formula discriminant = (b*b) – (4*a*c).
- Compute roots based on the nature of discriminant.
- If
discriminant > 0then,
root1 = (-b + sqrt(discriminant)) / (2*a)and
root2 = (-b - sqrt(discriminant)) / (2*a).Learn – Program to find square root of a number using sqrt() function.
- If
discriminant == 0then,root1 = root2 = -b / (2*a). - Else if
discriminant < 0then, there are two distinct complex roots where
root1 = -b / (2*a)androot2 = -b / (2*a).Imaginary part of the root is given by
imaginary = sqrt(-discriminant) / (2*a).
After this much reading let us finally code the solution of this program.
Program to find roots of quadratic equation
/**
* C program to find all roots of a quadratic equation
*/
#include <stdio.h>
#include <math.h> /* Used for sqrt() */
int main()
{
float a, b, c;
float root1, root2, imaginary;
float discriminant;
printf("Enter values of a, b, c of quadratic equation (aX^2 + bX + c): ");
scanf("%f%f%f", &a, &b, &c);
/* Find discriminant of the equation */
discriminant = (b * b) - (4 * a * c);
/* Find the nature of discriminant */
if(discriminant > 0)
{
root1 = (-b + sqrt(discriminant)) / (2*a);
root2 = (-b - sqrt(discriminant)) / (2*a);
printf("Two distinct and real roots exists: %.2f and %.2f", root1, root2);
}
else if(discriminant == 0)
{
root1 = root2 = -b / (2 * a);
printf("Two equal and real roots exists: %.2f and %.2f", root1, root2);
}
else if(discriminant < 0)
{
root1 = root2 = -b / (2 * a);
imaginary = sqrt(-discriminant) / (2 * a);
printf("Two distinct complex roots exists: %.2f + i%.2f and %.2f - i%.2f",
root1, imaginary, root2, imaginary);
}
return 0;
}Before you move on to next exercise. It is recommended to learn this program using another approach using switch...case.
Learn more – Program to find roots of quadratic equation using switch case.
Output
Enter values of a, b, c of quadratic equation (aX^2 + bX + c): 8 -4 -2 Two distinct and real roots exists: 0.81 and -0.31
Happy coding 😉
Recommended posts
- If else programming exercises index.
- C program to check whether a triangle is valid or not if all angles are given.
- C program to check whether a triangle is valid or not if sides are given.
- C program to find percentage and grade.
- C program to calculate gross salary of an employee.
- C program to calculate gross electricity bill.
- C program to find power of a number.