C program to find sum of upper triangular matrix

Categories C programming 2 mins read

Write a C program to read elements in a matrix and find sum of upper triangular matrix. How to find sum of upper triangular matrix in C. Logic to find sum of upper triangular matrix.

Example

Input

Input matrix elements: 
1 2 3
0 5 6
0 0 9

Output

Sum of upper triangular matrix = 11

Required knowledge

Basic C programming, For loop, Array

Must know – Program to find upper triangular matrix

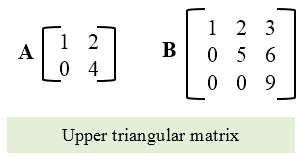
Upper triangular matrix

Upper triangular matrix is a special square matrix whose all elements below main diagonal is zero.

Upper triangular matrix

Logic to find sum of upper triangular matrix

Sum of upper triangular matrix is denoted with below image. In below image we need to find sum of matrix elements inside the red triangle.

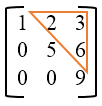
Upper triangular matrix elements

Formula to find sum of all elements matrix A inside the red triangular area is given by –
sum = sum + Aij (Where i<j).

Read more – Program to find sum of lower triangular matrix

Program to find sum of upper triangular matrix

/**
 * C program to find sum of upper triangular matrix
 */

#include <stdio.h>
#define MAX_ROWS 3
#define MAX_COLS 3

int main()
{
    int A[MAX_ROWS][MAX_ROWS];
    int row, col, sum = 0;
    
    /* Input elements in matrix from user */
    printf("Enter elements in matrix of size %dx%d: \n", MAX_ROWS, MAX_COLS);
    for(row=0; row<MAX_ROWS; row++)
    {
        for(col=0; col<MAX_COLS; col++)
        {
            scanf("%d", &A[row][col]);
        }
    }
    
    /* Find sum of upper triangular matrix */
    for(row=0; row<MAX_ROWS; row++)
    {
        for(col=0; col<MAX_COLS; col++)
        {
            if(col>row)
            {
                sum += A[row][col];
            }
        }
    }

    printf("Sum of upper triangular matrix = %d", sum);

    return 0;
}

Output

Enter elements in matrix of size 3x3:
1 2 3
0 5 6
0 0 9
Sum of upper triangular matrix = 11

Happy coding 😉