Write a C program to read elements in two matrices and add elements of both matrices. C program for addition of two matrix. Matrix addition program in C. Logic to add two matrix in C programming.
Example
Input
Input elements in 3x3 matrix1: 1 2 3 4 5 6 7 8 9 Input elements in 3x3 matrix2: 9 8 7 6 5 4 3 2 1
Output
Sum of both matrix = 10 10 10 10 10 10 10 10 10
Required knowledge
Basic C programming, For loop, Array
Matrix Addition
Matrix addition is done element wise (entry wise) i.e. Sum of two matrices A and B of size mXn is defined by
(A + B) = Aij + Bij (Where 1 ≤ i ≤ m and 1 ≤ j ≤ n)
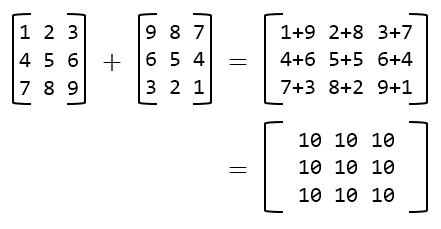
Program to add two matrices
/**
* C program to find sum of two matrices of size 3x3
*/
#include <stdio.h>
#define SIZE 3 // Size of the matrix
int main()
{
int A[SIZE][SIZE]; // Matrix 1
int B[SIZE][SIZE]; // Matrix 2
int C[SIZE][SIZE]; // Resultant matrix
int row, col;
/* Input elements in first matrix*/
printf("Enter elements in matrix A of size 3x3: \n");
for(row=0; row<SIZE; row++)
{
for(col=0; col<SIZE; col++)
{
scanf("%d", &A[row][col]);
}
}
/* Input elements in second matrix */
printf("\nEnter elements in matrix B of size 3x3: \n");
for(row=0; row<SIZE; row++)
{
for(col=0; col<SIZE; col++)
{
scanf("%d", &B[row][col]);
}
}
/*
* Add both matrices A and B entry wise or element wise
* and stores result in matrix C
*/
for(row=0; row<SIZE; row++)
{
for(col=0; col<SIZE; col++)
{
/* Cij = Aij + Bij */
C[row][col] = A[row][col] + B[row][col];
}
}
/* Print the value of resultant matrix C */
printf("\nSum of matrices A+B = \n");
for(row=0; row<SIZE; row++)
{
for(col=0; col<SIZE; col++)
{
printf("%d ", C[row][col]);
}
printf("\n");
}
return 0;
}Output
Enter elements in matrix A of size 3x3: 1 2 3 4 5 6 7 8 9 Enter elements in matrix B of size 3x3: 9 8 7 6 5 4 3 2 1 Sum of matrices A+B = 10 10 10 10 10 10 10 10 10
Happy coding 😉
