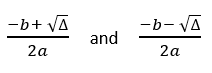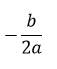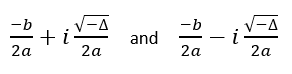C program to find all roots of a quadratic equation using switch case

Write a C program to find all roots of a Quadratic equation using switch case. How to find all roots of a quadratic equation using switch case in C programming. Logic to calculate roots of quadratic equation in C program.

Input a: 4
Input b: -2
Input c: -10

Root1: 1.85
Root2: -1.35

Required knowledge

Basic C programming, Relational operators, Switch case statement

Learn more – Program to find roots of quadratic equation using if…else.

Quadratic equation

In elementary algebra quadratic equation is an equation in the form of

Solving quadratic equation

A quadratic equation can have either one or two distinct real or complex roots depending upon nature of discriminant of the equation. Where discriminant of the quadratic equation is given by

Depending upon the nature of the discriminant, formula for finding roots can be given as:

• Case 1: If discriminant is positive. Then there are two real distinct roots given by.
  
• Case 2: If discriminant is zero. Then it have exactly one real root given by.
  
• Case 3: If discriminant is negative. Then it will have two distinct complex roots given by.
  

Logic to find roots of quadratic equation using switch...case

Step by step descriptive logic to find roots of quadratic equation using switch case.

1. Input coefficients of quadratic equation. Store it in some variable say a, b and c.
2. Find discriminant of given equation using formula i.e. discriminant = (b * b) - (4 * a * c).
   You can also use pow() function to find square of b.
3. Compute the roots based on the nature of discriminant. Switch the value of switch(discriminant > 0).
4. The expression (discriminant > 0) can have two possible cases i.e. case 0 and case 1.
5. For case 1 means discriminant is positive. Apply formula root1 = (-b + sqrt(discriminant)) / (2*a); to compute root1 and root2 = (-b - sqrt(discriminant)) / (2*a); to compute root2.
   

   Learn more – Program to find square root of a number.

6. For case 0 means discriminant is either negative or zero. There exist one more condition to check i.e. switch(discriminant < 0).
7. Inside case 0 switch the expression switch(discriminant < 0).
8. For the above nested switch there are two possible cases. Which is case 1 and case 0. case 1 means discriminant is negative. Whereas case 0 means discriminant is zero.
9. Apply the formula to compute roots for both the inner cases.

Program to find roots of quadratic equation using switch...case

/**
 * C program to find all roots of a quadratic equation using switch case
 */

#include <stdio.h>
#include <math.h> /* Used for sqrt() */

int main()
{
    float a, b, c;
    float root1, root2, imaginary;
    float discriminant;

    printf("Enter values of a, b, c of quadratic equation (aX^2 + bX + c): ");
    scanf("%f%f%f", &a, &b, &c);

    /* Calculate discriminant */
    discriminant = (b * b) - (4 * a * c);


    /* Compute roots of quadratic equation based on the nature of discriminant */
    switch(discriminant > 0)
    {
        case 1:
            /* If discriminant is positive */
            root1 = (-b + sqrt(discriminant)) / (2 * a);
            root2 = (-b - sqrt(discriminant)) / (2 * a);

            printf("Two distinct and real roots exists: %.2f and %.2f", 
                    root1, root2);
            break;

        case 0:
            /* If discriminant is not positive */
            switch(discriminant < 0)
            {
                case 1:
                    /* If discriminant is negative */
                    root1 = root2 = -b / (2 * a);
                    imaginary = sqrt(-discriminant) / (2 * a);

                    printf("Two distinct complex roots exists: %.2f + i%.2f and %.2f - i%.2f", 
                            root1, imaginary, root2, imaginary);
                    break;

                case 0:
                    /* If discriminant is zero */
                    root1 = root2 = -b / (2 * a);

                    printf("Two equal and real roots exists: %.2f and %.2f", root1, root2);

                    break;
            }
    }

    return 0;
}

Enter values of a, b, c of quadratic equation (aX^2 + bX + c): 4 -2 -10
Two distinct and real roots exists: 1.85 and -1.35

Happy coding 😉